Je mets à disposition sur cette page web différents petits projets réalisés à l'ESSTIN puis par moi-même avec le logiciel Fluent. Cinq sections regroupent ces projets :
- 1. projets 2D (2)
- 2. projet 2D en dynamique
- 3. projet 3D en maillage tournant
- 4. projets 3D en maillage fixe (2)
- 5. projet 3D en diphasique

1.a) Jet rond libre
Ce sujet concerne un jet rond libre, donc une simulation de mécanique des fluides axisymétrique.
Vous trouverez en fichier à télécharger sur le lien ci dessous, un maillage réalisé sous Gambit pour simuler ce jet rond libre. Il ne vous reste qu'à exporter ce fichier en .msh pour pouvoir travailler avec Fluent. Il s'agit d'un maillage structuré en 2D, assez simple à réaliser puisque les formes sont rectangulaires.
maillage pour gambit (Fichier Journal 3 Ko)

La modélisation sous Fluent prend en compte un profil de vitesse turbulent en entrée (UDF) et un modèle k-epsilon pour la turbulence.
Il est important de remarquer que lors du paramétrage du solver 2D, il faut activer la case "Axisymmetric".
De plus le modèle de turbulence est un peu particulier pour ce jet (Define --> Models --> Viscous --> k-epsilon), car le gradient de vitesse en sortie peut être important à cause du cisaillement de l'air ambiant : cocher la case "k-epsilon Model Realizable". Enfin à cause de la couche limite, cocher la case "Enhanced Wall Treatment".
Concernant la condition limite en entrée, l'intensité turbulente au centre du jet doit être d'environ 20%, avec une échelle de longueur de l'ordre du diamètre du tube.

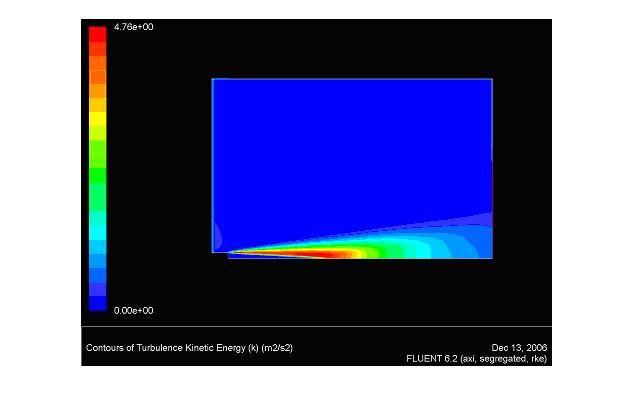
Vous pouvez voir ci-dessous deux résultats de la simulation :
- énergie cinétique turbulente k
- les lignes de courant à proximité de la sortie du tube

énergie cinétique turbulente k

Qualitativement on constate bien vers l’extrémité « haute » du jet à la sortie du tube, une production de turbulence. A ce niveau un cisaillement se produit dans l’air ambiant, dû à l’arrivée du jet sortant du tube, et un cône potentiel apparaît en bout de tube dans le jet. Ce cône apparaît logiquement en bleu sur la figure ci dessus.

lignes de courant

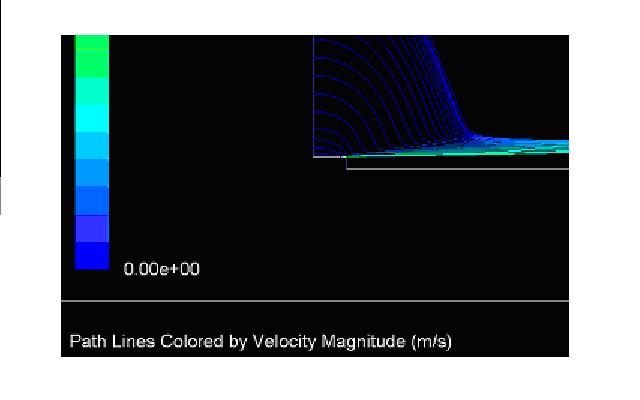
On constate que logiquement les lignes de courant tournent fortement puisqu'elles suivent le mouvement fluide dû au jet.

1.b) Profil d'aile
Ce sujet concerne un profil d'aile bidimensionnel NACA4315, donc un sujet traitant plus particulièrement d'aérodynamique.
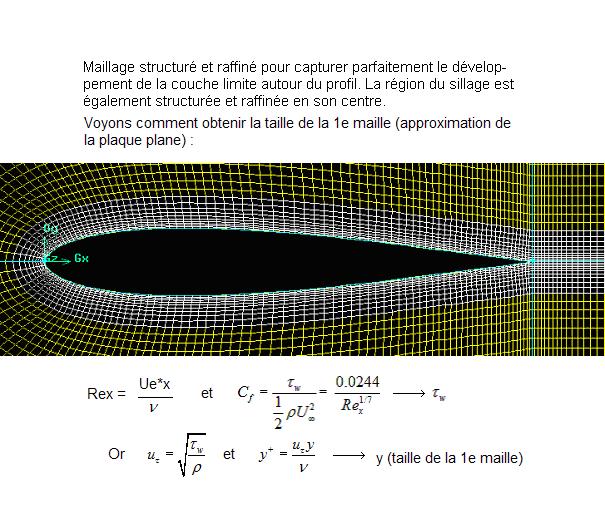
Le maillage doit être structuré et raffiné en proche paroi pour tenir compte du développement de la couche limite le long du profil. On sait par expérience que ce profil décroche vers 18°, ce que nous allons montrer par simulation avec Fluent.
Voici une image du maillage (zoom sur l'endroit structuré) :

Concernant la simulation avec Fluent, il suffit de configurer un solver 2D coupled (régime transsonique). A noter que l'on peut travailler en instationnaire aussi. Si on choisit le stationnaire, on reste en laminaire (Define --> Models --> Viscous --> Laminar). La condition d'entrée est une vitesse de Mach 0,8 et la pression de sortie est à l'infini.

Vous pouvez voir ci-dessous deux résultats de la simulation :
- répartition de pression
- décollement de la C.L. à l'aval -au bord de fuite- avec une assiette de 30° --> phénomène de décrochage

répartition de pression

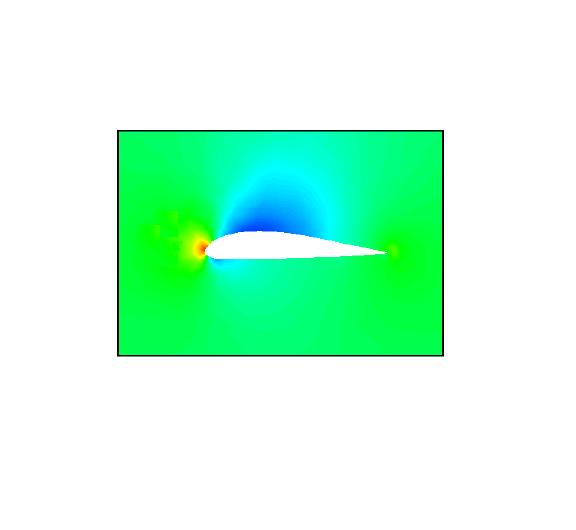
Qualitativement on constate bien un point d'arrêt vers le bord d'attaque puis une sur-vitesse marquée (donc sous-pression) sur l'extrados. Comme le profil est non symétrique, il a une légère portance même à assiette nulle. Il n'y a pas de mini onde de choc locale, détectée par la simulation à M = 0,8.

décrochage

L'expérience montre que ce profil NACA 4315 décroche à 18°. La simulation numérique avec Fluent donne elle le décrochage à 21°. C'est un résultat satisfaisant. Il y a deux méthodes pour visualiser ce décrochage : soit un décollement de la couche limite au bord de fuite (sillage devient important), soit une recirculation au bord de fuite. C'est cette deuxième caractéristique que vous voyez sur l'image ci-dessus : le profil est soumis à un angle d'attaque de 30° pour bien voir ce phénomène.

2. Aile battante
Ce sujet est utile pour des études de drones à ailes battantes. Il se base aussi sur le profil NACA 4315.
Le maillage est réalisé sous Gambit en 2D toujours. Il est constitué de deux zones : une zone structurée et raffinée proche du profil, et une zone entourant la première structurée simplement. Un interface sépart les deux zones!

La modélisation sous Fluent prend en compte une UDF définissant le mouvement dit "battant" de l'aile. En fait c'est la zone structurée et raffinée autour du profil qui va être animée d'un mouvement par rapport à la zone extérieure fixe : le mouvement est celui décrit par le profil grâce à une UDF que vous pouvez récupérer sur le lien suivant.
UDF pour Fluent (Fichier .c 1 Ko)
Une fois que l'UDF est compilée sous Fluent (Define --> User-Defined --> Functions --> Compiled, puis cliquer sur "Build" puis "Load"), allez dans Define --> Dynamic Mesh --> Parameters. Là, sélectionnez : Dynamic Mesh. Un menu nouveau est maintenant disponible : Define --> Dynamic Mesh --> Zones.
La fenêtre Dynamic Zones vous permet de sélectionner le type de zone dynamique que vous voulez utiliser : sélectionnez "Rigid Body". Dans Zone Names selectionnez la zone mobile. Dans Motion Attributes doit apparaitre l'UDF compilée précédement. Il ne reste plus qu'à indiquer la position du centre de gravité et à cliquer sur Create.
Il s'agit maintenant de reconstituer le maillage : Define --> Dynamic Mesh --> Parameters.
Pour cet exemple cliquez sur "Smoothing" & "Remeshing". Il est intéressant de voir les différents paramètres, de jouer sur les valeurs, afin de trouver le meilleur compromis. Il est possible de tester les paramètres de remaillage ainsi que le mouvement donné à la zone mobile sans exécuter le calcul (énorme gain de temps). Pour celà, allez dans le menu : Solve --> mesh motion. Cette fenêtre vous permet de visualiser l'évolution du maillage au cours du temps. Attention il faut bien sauvegarder avant et surtout ne pas sauvegarder après , car le maillage serait enregistré dans sa configuration déformée...

Concernant les paramètres de simulation numérique : on configure un solver 2D segregated instationnaire. Puis pour la turbulence : Define --> Models --> Viscous --> k-epsilon. Les conditions limites sont une pression à l'infini en sortie et une vitesse en entrée modérée (10 à 15 m/s). Il est conseillé de limiter le ratio de viscosité turbulente sur viscosité au repos à 10.

Vous avez ci-dessous un lien vers une vidéo (plus intéressante en terme de vision d'un résultat dynamique) réalisée par l'ONERA dans le cadre du projet Remanta. Jouez la 7e et dernière vidéo :
vidéo d'une aile battante (projet REMANTA)

3. Pompe centrifuge
Ce sujet concerne une étude simplifiée d'une pompe centrifuge. L'idée est de caractériser la présence de vortex en bout d'aubage, pour pouvoir adapter au mieux leur longueur.
Il s'agit d'un maillage tournant 3D dont les différents volumes sont montrés sur la figure ci dessous en vue en coupe de côté :

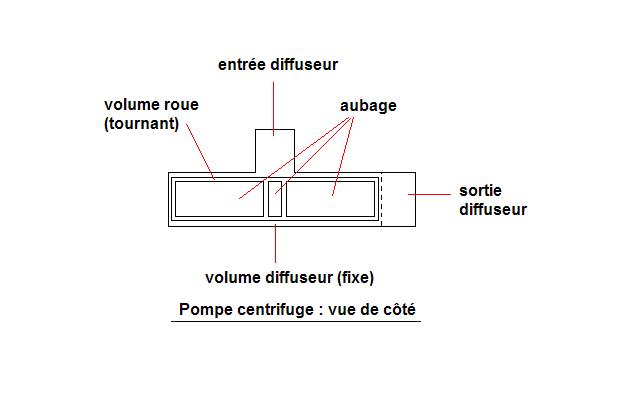
Sous Gambit, il faut définir deux interfaces distinctes mais paradoxalement au même endroit (les faces sont différentes --> cocher "Retain" lors du "split" des volumes). A noter que le petit volume doit être inclus totalement dans le grand. Une fois ces deux conditions limites supplémentaires définies, il faut définir deux volumes fluide distincts : un sera tournant et l'autre fixe. Un volume fluide peut être constitué de plusieurs sous-volumes (intéressant pour raffiner des zones). Il n'est pas nécessaire de structurer ce maillage.

Le paramétrage de Fluent passe bien sûr par un solver 3D unsteady ici. Il est utile de diminuer les facteurs de relaxation de la pression et de k - énergie cinétique turbulente.
Le modèle de turbulence peut être un k-epsilon, avec une échelle de longueur égale à la corde d'une l'aubage. Enfin cliquer sur Define --> Grid Interfaces et créer une interface commune (des murs virtuels sont ajoutés par Fluent). Dans Boundary Conditions, cliquer sur votre volume tournant puis "Set" et choisir l'option "Moving Mesh". Il reste à paramétrer la vitesse de rotation selon l'axe désiré.

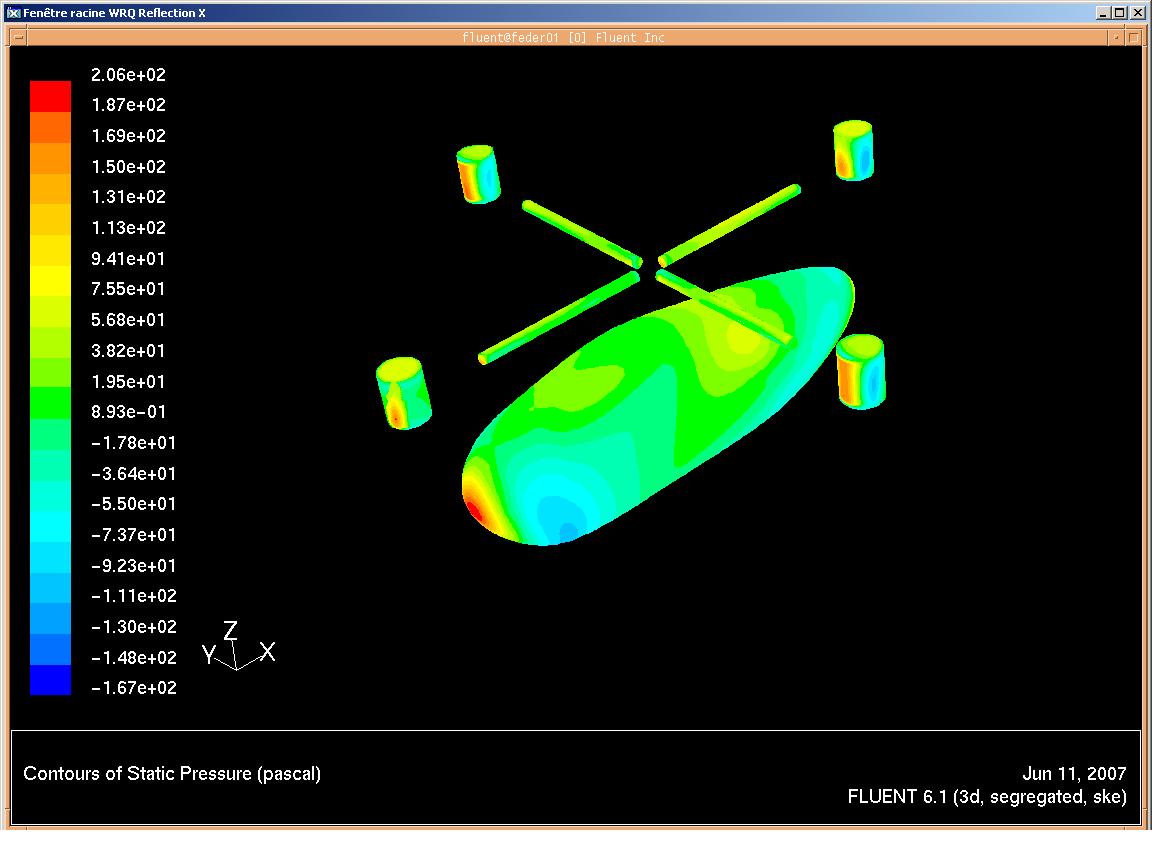
Vous pouvez voir ci-dessous deux résultats de la simulation :
- répartition de pression
- vortex

répartition de pression

vortex

On peut rapidement vérifier si le modèle est correct en calculant I (intensité turbulente). Je parle ici en valeur moyenne : k = 9.5m²/s² et U = (pi*N/30)*R/2 = 25m/s. Donc I = 10% ce qui est valable.

4.a) Fuselage
Ce sujet concerne l'étude d'un corps profilé pour les bas nombres de Reynolds. Il permet de comprendre la difficulté de structurer une partie de maillage (celle pour la couche limite) quand la géométrie est complexe. De plus nous verrons quelques considérations sur la "taille mémoire".
Le maillage est hybride 3D : il est structuré et raffiné en proche paroi ce qui est aisé avec des formes simples (des cylindres par exemple), mais plus compliqué avec une forme complexe (le fuselage présenté plus bas sur la photo). Tout en gardant la méthode de création de géométrie d'un fichier Gambit (à savoir création de tous les volumes, puis "split" du plus extérieur vers le plus intérieur), il faut découper le volume de contrôle fin autour du fuselage par des faces. Ainsi on obtient des guides 2D qui vont permettre un maillage structuré et raffiné.
Un autre point important est d'imbriquer plusieurs volumes dans la zone non-structurée afin d'augmenter progressivement la taille des mailles (en allant de plus en plus loin des parois) et aussi de limiter le nombre de mailles par volume. Il faut savoir que 1 Million de mailles tétraédriques consomme 340 Mo de RAM . Il est conseillé aussi d'augmenter parfois la zone de SWAP de son PC.

Le paramétrage de Fluent passe par un solver 3D segregated. Choisir un modèle de turbulence k-epsilon (Define --> Models --> Viscous --> k-epsilon) en cochant : "Enhanced Wall Treatment". Renseigner le matériau du fuselage comme étant du PVC. Pour les conditions limites, utiliser :
- en sortie, pression à l'infini pour un ratio limité de 10 (viscosité turbulente sur viscosité au repos) et I = 1%
- en entrée, vitesse désirée pour un ratio limité de 10 (viscosité turbulente sur viscosité au repos) et I = 1%
- pression désirée en entrée sur les rotors, et une échelle de turbulence en longueur égale à la corde d'une pale (I = 5%)

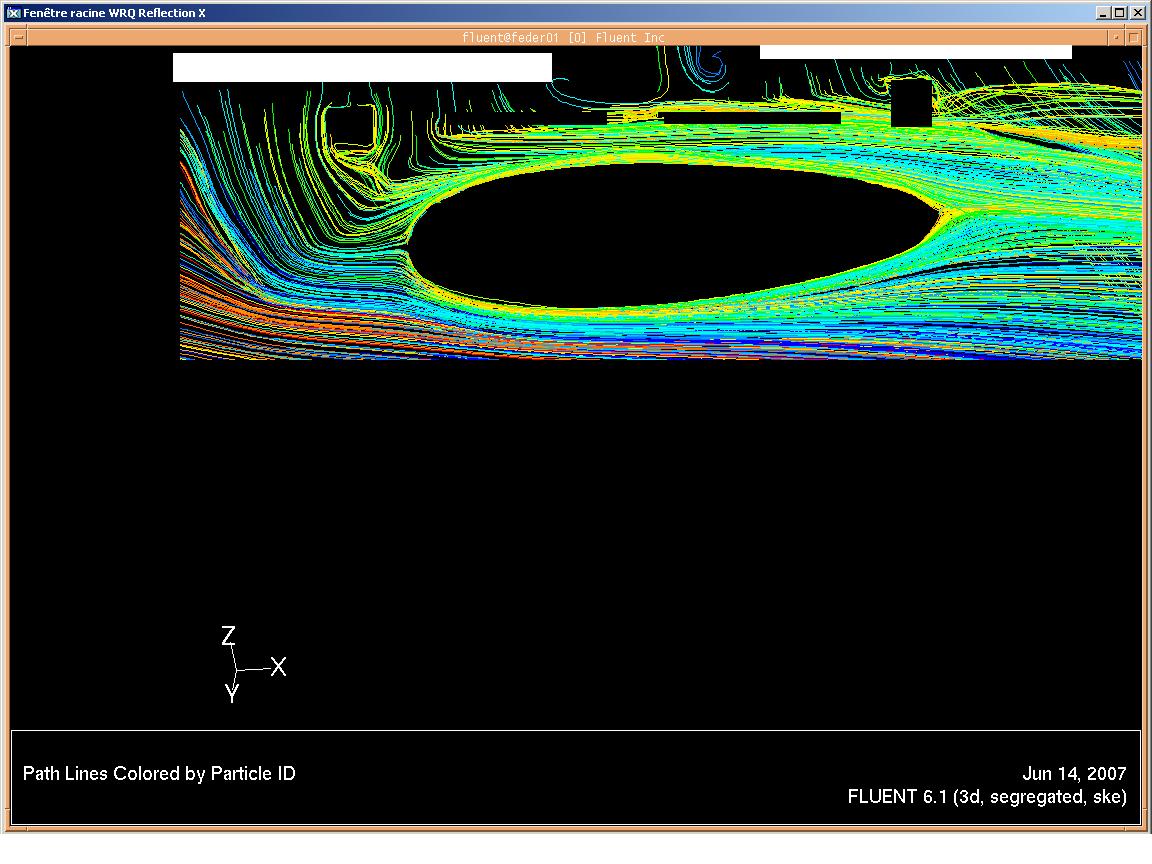
Vous pouvez voir ci-dessous deux résultats de la simulation :
- répartition de pression
- lignes de courant

répartition de pression

lignes de courant

4.b) Echangeur de chaleur co-courant (influence de la turbulence)
Ce sujet porte sur du transfert de chaleur. Il concerne un échangeur de chaleur tubulaire, et introduit quelques bases du post-processing sous Fluent.
La géométrie est un tube extérieur percé par un tube intérieur. Le maillage est 3D structuré, et raffiné au niveau de la paroi séparant les deux tubes. La capture de la couche limite se développant de chaque côté de cette paroi est très importante.

Concernant le paramétrage de la simulation numérique avec Fluent, on utilise un solver 3D segregated. Là encore on choisit un modèle de turbulence k-epsilon (Define --> Models --> Viscous --> k-epsilon) en cochant : "Enhanced Wall Treatment" et "Thermal Effects". Le renseignement des matériaux est extrêmement important : tubes en aluminium. Le fluide est évidemment de l'eau. Lors de la définition des conditions aux limites, cliquer sur "Wall" puis "Set" et renseigner sur l'épaisseur des parois. C'est un échangeur co-courant donc faire entrer une eau à 80°C au centre, qui est refroidie par une eau à 20°C dans le tube extérieur. Utiliser les diamètres hydrauliques pour la turbulence en entrée. Appliquer un débit supérieur d'eau froide afin de maintenir l'eau vers 20°C dans le tube extérieur. Créer enfin un plan longitudinal qui va servir au post-processing de Fluent.

Vous pouvez voir ci-dessous deux résultats de la simulation :
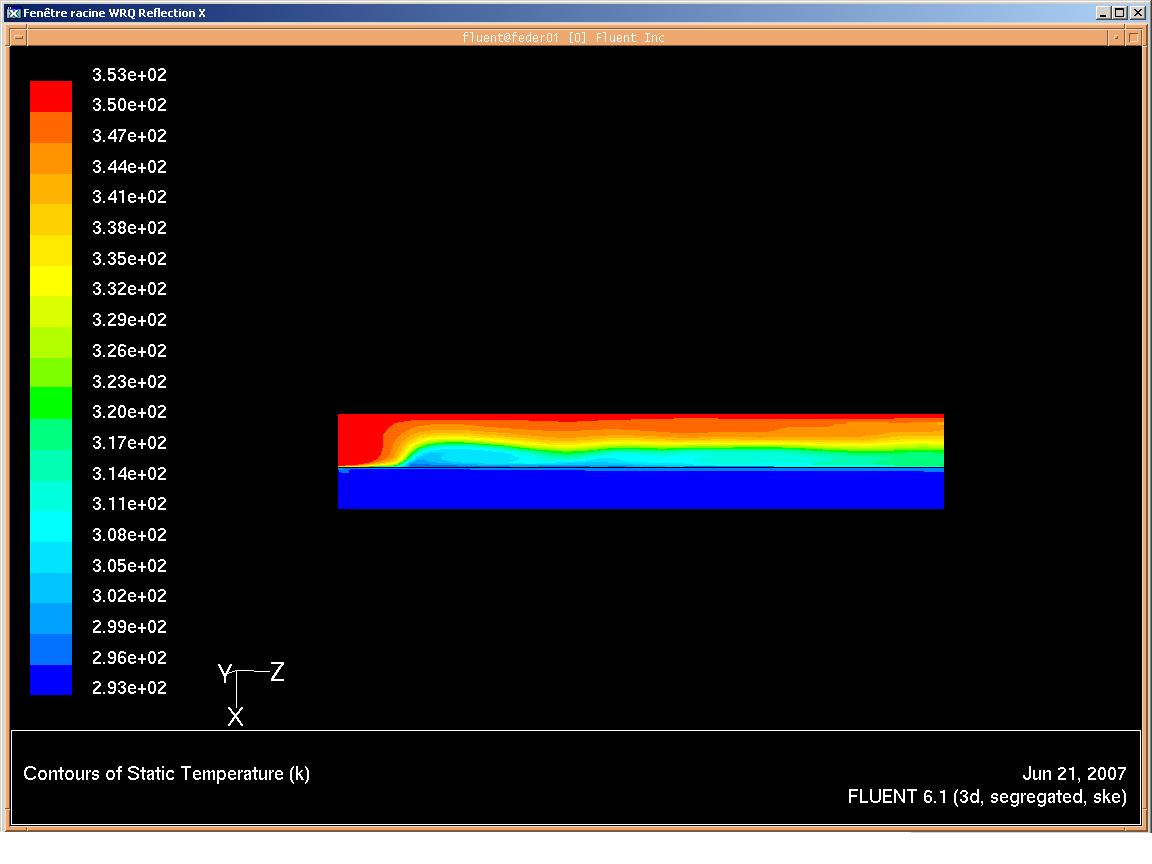
- vue du champ de température dans le plan de coupe
- courbe montrant l'évolution de la température sur la longueur

champ de température

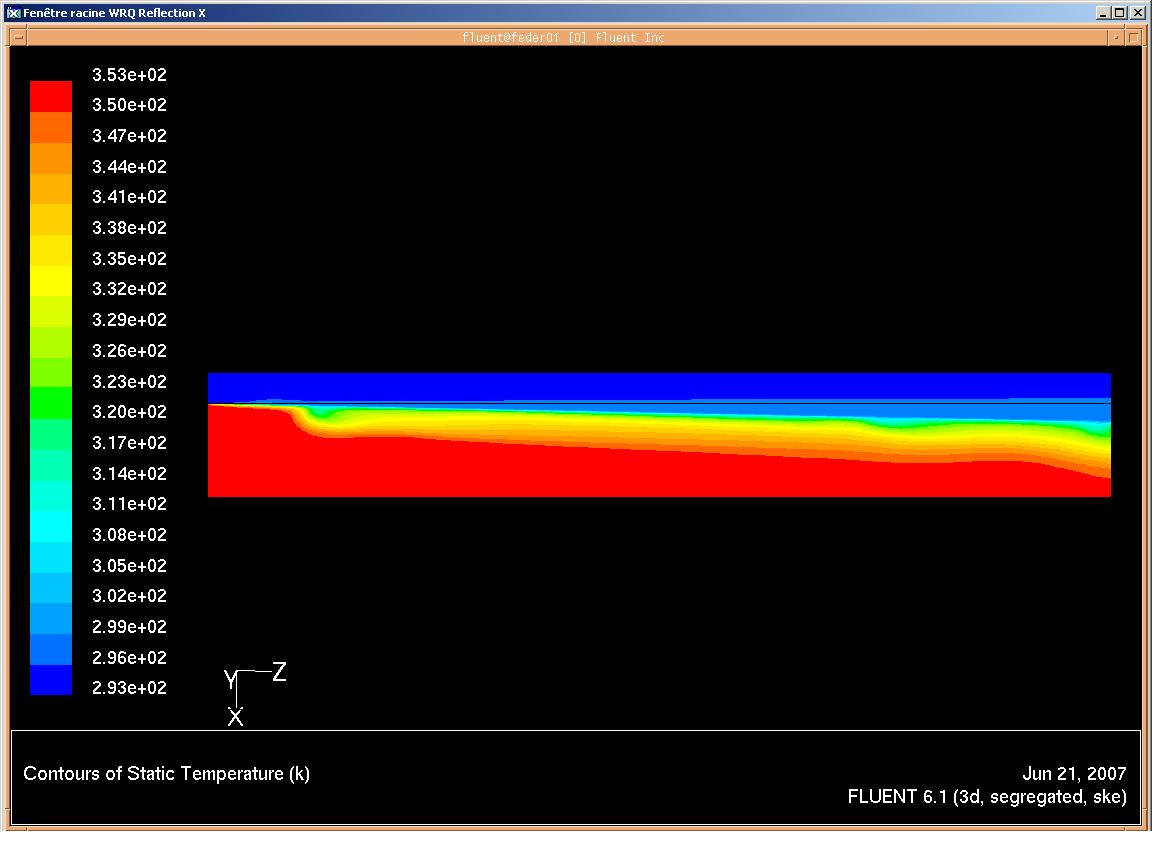
évolution de température en longitudinal

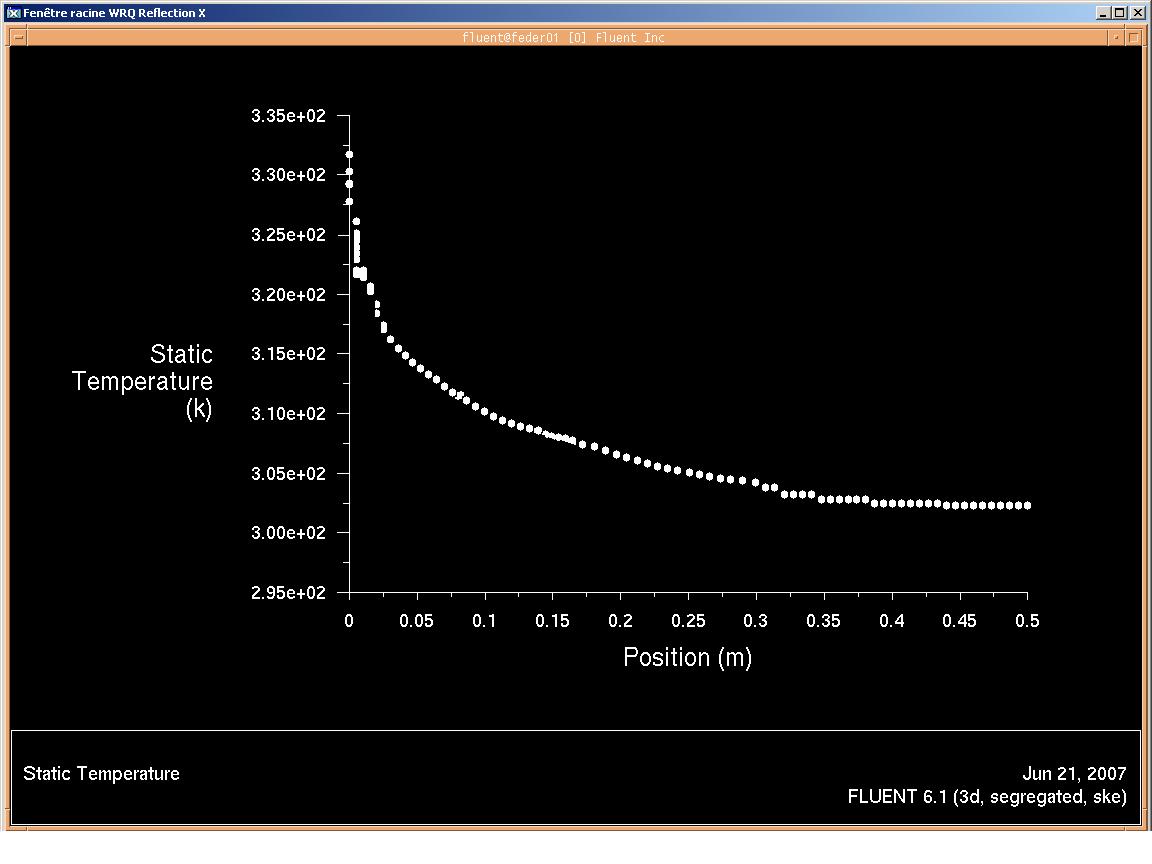
Le profil de température ci-dessus est pris dans le tube intérieur (chaud) à 1 mm de la paroi. On passe en 50 cm d'une température de 80°C (353 K) à 30°C (303 K). Le plus intéressant est qu'en moins de 10 cm on passe de 80°C (353 K) à 40°C (313 K), soit une diminution significative. Ce phénomène s'observe dans la couche limite laminaire, siège d'un transfert de chaleur important avec le tube extérieur froid (le refroidisseur). L'évolution de température vers le centre du tube intérieur est plus stratifiée, ce qui est caractéristique d'un régime laminaire d'écoulement.

On peut réaliser une deuxième simulation avec Fluent, en s'arrangeant pour que la couche limite devienne turbulente (meilleur échange de chaleur). Il suffit d'augmenter la rugosité en paroi. Si la couche limite turbulente se développe bien, alors après une bonne longueur de tuyau l'écoulement sera : totalement turbulent (ce cas ne nous intéresse pas ici - pour en connaître les caractéristiques, suivez le lien : cliquez ici).

Vous pouvez voir ci-dessous un résultat de la simulation :
- vue du champ de température dans le plan de coupe

champ de température

On passe de 80°C (353 K) à 40°C (313 K), soit une diminution significative, en 5 cm : deux fois plus rapide que dans l'exemple précédent! La couche limite est turbulente ce qui augmente encore la capacité du fluide à échanger de la chaleur. Le régime de strates est moins net, le liquide (l'eau ici) est refroidi plus vite. Vers la fin du tube (à droite sur le dessin), le régime d'écoulement devient totalement turbulent et commence à se caractériser par un champ de température diffus moyen (bulk en anglais).

5. Etude diphasique 3D
Un écoulement diphasique consiste en un écoulement avec deux phases souvent mélangées : liquide-vapeur ou liquide-solide. Pour avoir des renseignements sur ces écoulements et leur simulation, suivez le lien ci-dessous : étude diphasique

Quelques considérations sur la simulation numérique en général

Les logiciels de simulation numérique utilisés couramment par l'industrie (comme Fluent par exemple) utilisent les équations de Navier Stokes moyennées. Elles sont discrétisées selon l'espace et le temps puis résolues grâce à des méthodes diverses. Concernant la turbulence, elle est entièrement modélisée ce qui demande des modèles de fermeture. Les résultats sont donnés en tant que champs moyens ce qui n'est pas très précis. Par contre toutes sortes de géométries peuvent être modélisées. Il s'agit de calculs RANS. J'ai souvent utilisé les paramètres k-epsilon dans mes exemples ci-dessus pour approcher la turbulence (on pourrait utiliser k-omega). Ce sont des approches du premier ordre. Afin d'affiner ces calculs de turbulence, des approches au second ordre sont possibles (Rij-epsilon).

La recherche utilise de plus en plus la LES (Large Eddies Simulation). Le principe est de réaliser un filtrage des échelles de longueur de la turbulence, afin de calculer directement les grosses structures et de modéliser les petites. Le temps de calcul augmente, mais la caractérisation de la turbulence est bien meilleure. Enfin la simulation numérique directe (DNS) calcule elle directement toutes les échelles. Cependant celà nécessite un espace mémoire très important, ne s'applique actuellement qu'à de petits volumes simples et le temps de calcul est très long.